کارل گوستاو ژاکوب ژاکوبی
زندگی و دستاوردهای ژاکوبی ریاضیدان | نابغهای در توابع بیضوی، نظریه اعداد و ماتریس ژاکوبی که جهان ریاضی را متحول کرد
💡 ژاکوبی ریاضیدان: نابغهای از دنیای معادلات و توابع بیضوی 💪🧠
ژاکوبی ریاضیدان یکی از درخشانترین چهرههای تاریخ ریاضیات است که تأثیرات شگفتانگیزی در نظریه اعداد، توابع بیضوی، و جبر خطی گذاشته است. در این مقاله، به بررسی زندگی، دستاوردها و میراث ماندگار ژاکوبی ریاضیدان خواهیم پرداخت و دلیل اهمیت نام او در تاریخ علم را توضیح میدهیم.
🎯 زندگینامه ژاکوبی ریاضیدان
ژاکوبی ریاضیدان، با نام کامل کارل گوستاو یاکوب ژاکوبی (Carl Gustav Jacob Jacobi)، در سال ۱۸۰۴ در پُتسدام آلمان به دنیا آمد. از همان سنین کودکی، نبوغ ریاضیاتی ژاکوبی ریاضیدان بر همگان آشکار شد. او تحصیلات خود را در دانشگاه برلین ادامه داد و خیلی زود وارد عرصهی تدریس و تحقیق شد.
🧬 دستاوردهای علمی ژاکوبی ریاضیدان
✅ توابع بیضوی و ژاکوبی
یکی از مهمترین دستاوردهای ژاکوبی ریاضیدان، توسعه و تعمیم توابع بیضوی است. او این توابع را برای حل معادلات دیفرانسیل خاصی توسعه داد که در فیزیک و مهندسی کاربردهای فراوانی دارند.
✅ نظریه دترمینان ژاکوبی
ژاکوبی ریاضیدان همچنین مفهومی را توسعه داد که امروزه به نام "دترمینان ژاکوبی" (Jacobian Determinant) شناخته میشود و در حساب چندمتغیره کاربرد فراوان دارد. این نظریه پایهای برای آنالیز برداری و تبدیل مختصات است.
✅ تأثیر در نظریه اعداد
در حوزه نظریه اعداد نیز ژاکوبی ریاضیدان نقش بسزایی داشت. او با کارهایش بر روی تابع تتا و روابط آن با فرمهای مربعی، راه را برای ریاضیدانان آینده مانند رامانوجان هموار کرد.
💪 ژاکوبی ریاضیدان و دنیای امروز
امروزه نام ژاکوبی ریاضیدان در کتابهای درسی، مقالات علمی و الگوریتمهای محاسباتی دیده میشود. مفاهیمی مانند ماتریس ژاکوبی، تابع ژاکوبی، و روش ژاکوبی در حل دستگاه معادلات خطی، همگی نشاندهندهی وسعت تأثیر او در ریاضیات نوین هستند.
🩸 میراث علمی ژاکوبی ریاضیدان
ژاکوبی ریاضیدان تنها یک نظریهپرداز نبود، بلکه الهامبخش نسلی از ریاضیدانان شد. میراث او تا امروز زنده است و در هر گوشهای از ریاضیات میتوان نشانی از ذهن خلاق و پرتوان ژاکوبی ریاضیدان یافت.
🎓 چرا ژاکوبی ریاضیدان هنوز مهم است؟
-
✅ بنیانگذار توابع بیضوی
-
✅ پیشگام در آنالیز ریاضی
-
✅ الهامبخش تحقیقات مدرن
-
✅ تاثیرگذار بر فیزیک نظری و ریاضیات کاربردی
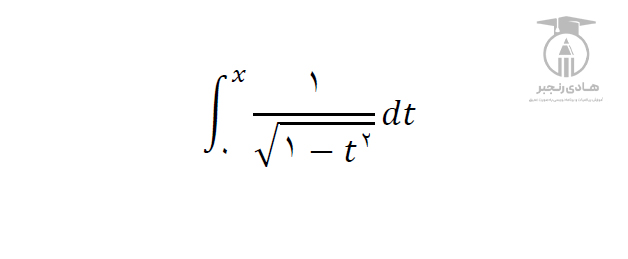
دیدگاه های مربوط به این مقاله (برای ارسال دیدگاه در سایت حتما باید عضو باشید و پروفایل کاربری شما تکمیل شده باشد)